4.5 Use the slope–intercept form of an equation of a line (Page 7/12)

<< Chapter < Page

Elementary algebra

Page 7 / 12

Chapter >> Page >

Use slopes and y -intercepts to determine if the lines $x = 1$ and $x = −5$ are parallel.

parallel

Got questions? Get instant answers now!

Use slopes and y -intercepts to determine if the lines $x = 8$ and $x = −6$ are parallel.

parallel

Got questions? Get instant answers now!

Use slopes and y -intercepts to determine if the lines $y = 2 x - 3$ and $−6 x + 3 y = −9$ are parallel. You may want to graph these lines, too, to see what they look like.

Solution

$\begin{matrix} \begin{matrix} The first equation is already in slope–intercept form. \\ Solve the second equation for y . \end{matrix} & \begin{matrix} y & = & 2 x - 3 \\ y & = & 2 x - 3 \\ - 6 x + 3 y & = & −9 \\ 3 y & = & 6 x - 9 \\ \frac{3 y}{3} & = & \frac{6 x - 9}{3} \end{matrix} & \begin{matrix} and \end{matrix} & \begin{matrix} −6 x + 3 y = −9 \end{matrix} \\ \begin{matrix} The second equation is now in \\ slope–intercept form. \\ Identify the slope and y -intercept of both lines. \end{matrix} & \begin{matrix} y & = & 2 x - 3 \\ y & = & 2 x - 3 \\ y & = & m x + b \\ m & = & 2 \end{matrix} & \begin{matrix} y & = & 2 x - 3 \\ y & = & m x + b \\ m & = & 2 \end{matrix} \\ y -intercept is (0 ,−3) & y -intercept is (0, −3) \end{matrix}$

The lines have the same slope, but they also have the same y -intercepts. Their equations represent the same line. They are not parallel; they are the same line.

Got questions? Get instant answers now!

Use slopes and y -intercepts to determine if the lines $y = - \frac{1}{2} x - 1$ and $x + 2 y = 2$ are parallel.

not parallel; same line

Got questions? Get instant answers now!

Use slopes and y -intercepts to determine if the lines $y = \frac{3}{4} x - 3$ and $3 x - 4 y = 12$ are parallel.

not parallel; same line

Got questions? Get instant answers now!

Use slopes to identify perpendicular lines

Let’s look at the lines whose equations are $y = \frac{1}{4} x - 1$ and $y = −4 x + 2$ , shown in [link] .

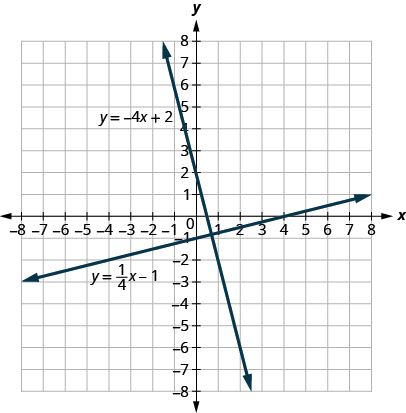
The figure shows two lines graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 8 to 8. The y-axis of the plane runs from negative 8 to 8. One line is labeled with the equation y equals negative 4x plus 2 and goes through the points (0,2) and (1, negative 2). The other line is labeled with the equation y equals one fourth x minus 1 and goes through the points (0, negative 1) and (4,0).

These lines lie in the same plane and intersect in right angles. We call these lines perpendicular .

What do you notice about the slopes of these two lines? As we read from left to right, the line $y = \frac{1}{4} x - 1$ rises, so its slope is positive. The line $y = −4 x + 2$ drops from left to right, so it has a negative slope. Does it make sense to you that the slopes of two perpendicular lines will have opposite signs?

If we look at the slope of the first line, $m_{1} = \frac{1}{4}$ , and the slope of the second line, $m_{2} = −4$ , we can see that they are negative reciprocals of each other. If we multiply them, their product is $−1 .$

\begin{matrix} m_{1} \cdot m_{2} \\ \frac{1}{4} (−4) \\ - 1 \end{matrix}

This is always true for perpendicular lines and leads us to this definition.

Perpendicular lines

Perpendicular lines are lines in the same plane that form a right angle.

If $m_{1} and m_{2}$ are the slopes of two perpendicular lines, then:

m_{1} \cdot m_{2} = −1 and m_{1} = \frac{−1}{m_{2}}

Vertical lines and horizontal lines are always perpendicular to each other.

We were able to look at the slope–intercept form of linear equations and determine whether or not the lines were parallel. We can do the same thing for perpendicular lines.

We find the slope–intercept form of the equation, and then see if the slopes are negative reciprocals. If the product of the slopes is $−1$ , the lines are perpendicular. Perpendicular lines may have the same y -intercepts.

Use slopes to determine if the lines, $y = −5 x - 4$ and $x - 5 y = 5$ are perpendicular.

Solution

$\begin{matrix} The first equation is in slope–intercept form. & y & = & −5 x - 4 \\ Solve the second equation for y . & x - 5 y & = & 5 \\ - 5 y & = & − x + 5 \\ \frac{−5 y}{−5} & = & \frac{− x + 5}{−5} \\ y & = & \frac{1}{5} x - 1 \\ Identify the slope of each line. & y & = & −5 x - 4 & y & = & \frac{1}{5} x - 1 \\ y & = & m x + b & y & = & m x + b \\ m_{1} & = & −5 & m_{2} & = & \frac{1}{5} \end{matrix}$

The slopes are negative reciprocals of each other, so the lines are perpendicular. We check by multiplying the slopes,

\begin{matrix} m_{1} \cdot m_{2} \\ - 5 (\frac{1}{5}) \\ - 1 ✓ \end{matrix}

Got questions? Get instant answers now!

Use slopes to determine if the lines $y = −3 x + 2$ and $x - 3 y = 4$ are perpendicular.

perpendicular

Got questions? Get instant answers now!

Use slopes to determine if the lines $y = 2 x - 5$ and $x + 2 y = −6$ are perpendicular.

perpendicular

Got questions? Get instant answers now!

Use slopes to determine if the lines, $7 x + 2 y = 3$ and $2 x + 7 y = 5$ are perpendicular.

Solution

$\begin{matrix} Solve the equations for y . & 7 x + 2 y & = & 3 & 2 x + 7 y & = & 5 \\ 2 y & = & −7 x + 3 & 7 y & = & −2 x + 5 \\ \frac{2 y}{2} & = & \frac{−7 x + 3}{2} & \frac{7 y}{7} & = & \frac{−2 x + 5}{7} \\ y & = & - \frac{7}{2} x + \frac{3}{2} & y & = & - \frac{2}{7} x + \frac{5}{7} \\ Identify the slope of each line. & y & = & m x + b & y & = & m x + b \\ m_{1} & = & - \frac{7}{2} & m_{2} & = & - \frac{2}{7} \end{matrix}$

The slopes are reciprocals of each other, but they have the same sign. Since they are not negative reciprocals, the lines are not perpendicular.

Got questions? Get instant answers now!

<< Chapter < Page Page > Chapter >>

Practice Key Terms 3

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Elementary algebra. OpenStax CNX. Jan 18, 2017 Download for free at http://cnx.org/content/col12116/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Elementary algebra' conversation and receive update notifications?

Ask

	1 Understanding Societies 1 By Jessica Collett Start Exam
	20 Hemostasis Dr. Olver By Brooke Delaney Start Exam
	7 AP 07 Axial Skeleton Essay By OpenStax Start Flashcards
	16 AP 16 Neurological Essay Exam By OpenStax Start Flashcards
	46 Biology 46 Ecosystems MCQ By OpenStax Start Quiz
	12 AP Key Terms 12 The Nervous System By OpenStax Start Key Terms
©flickr: Jonathan	Power By Megan Earhart Start Quiz
	13 Biology 13 Modern Understandings of Inheritance By OpenStax Start Quiz
	Computer System Engineering By Robert Morris Start Exam
	42 Biology 42 The Immune System MCQ By OpenStax Start Quiz