| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
When you graph linear equations, you may notice that some lines tilt up as they go from left to right and some lines tilt down. Some lines are very steep and some lines are flatter. What determines whether a line tilts up or down or if it is steep or flat?
In mathematics, the ‘tilt’ of a line is called the slope of the line. The concept of slope has many applications in the real world. The pitch of a roof, grade of a highway, and a ramp for a wheelchair are some examples where you literally see slopes. And when you ride a bicycle, you feel the slope as you pump uphill or coast downhill.
In this section, we will explore the concept of slope.
A geoboard is a board with a grid of pegs on it. Using rubber bands on a geoboard gives us a concrete way to model lines on a coordinate grid. By stretching a rubber band between two pegs on a geoboard, we can discover how to find the slope of a line.
We’ll start by stretching a rubber band between two pegs as shown in [link] .
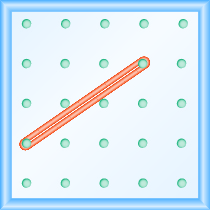
Doesn’t it look like a line?
Now we stretch one part of the rubber band straight up from the left peg and around a third peg to make the sides of a right triangle, as shown in [link]
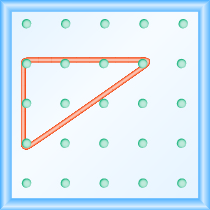
We carefully make a 90º angle around the third peg, so one of the newly formed lines is vertical and the other is horizontal.
To find the slope of the line, we measure the distance along the vertical and horizontal sides of the triangle. The vertical distance is called the rise and the horizontal distance is called the run , as shown in [link] .

If our geoboard and rubber band look just like the one shown in [link] , the rise is 2. The rubber band goes up 2 units. (Each space is one unit.)

What is the run?
The rubber band goes across 3 units. The run is 3 (see [link] ).
The slope of a line is the ratio of the rise to the run. In mathematics, it is always referred to with the letter .
The slope of a line of a line is .
The rise measures the vertical change and the run measures the horizontal change between two points on the line.
What is the slope of the line on the geoboard in [link] ?
The line has slope . This means that the line rises 2 units for every 3 units of run.
When we work with geoboards, it is a good idea to get in the habit of starting at a peg on the left and connecting to a peg to the right. If the rise goes up it is positive and if it goes down it is negative. The run will go from left to right and be positive.

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?