| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
Mathematicians like to look for patterns that will make their work easier. A good example of this is squaring binomials. While you can always get the product by writing the binomial twice and using the methods of the last section, there is less work to do if you learn to use a pattern.
Look at these results. Do you see any patterns?
What about the number of terms? In each example we squared a binomial and the result was a trinomial .
Now look at the first term in each result. Where did it come from?
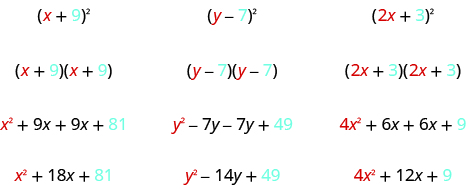
The first term is the product of the first terms of each binomial. Since the binomials are identical, it is just the square of the first term!
To get the first term of the product, square the first term .
Where did the last term come from? Look at the examples and find the pattern.
The last term is the product of the last terms, which is the square of the last term.
To get the last term of the product, square the last term .
Finally, look at the middle term . Notice it came from adding the “outer” and the “inner” terms—which are both the same! So the middle term is double the product of the two terms of the binomial.
To get the middle term of the product, multiply the terms and double their product .
Putting it all together:
If are real numbers,

To square a binomial:
A number example helps verify the pattern.
To multiply usually you’d follow the Order of Operations.
The pattern works!
Multiply:
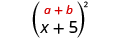 | |
| Square the first term. |
 |
| Square the last term. |
 |
| Double the product. |
 |
| Simplify. |
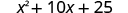 |
Multiply:
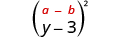 | |
| Square the first term. |
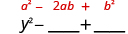 |
| Square the last term. |
 |
| Double the product. |
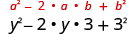 |
| Simplify. |
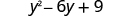 |

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?