| << Chapter < Page | Chapter >> Page > |
In [link] , we’ll start by using the Distributive Property. This step will clear the fractions right away!
Solve:
|
| |
| Distribute. |
|
| Simplify. Now there are no fractions to clear! |
|
| Subtract 1 from both sides. |
|
| Simplify. |
|
| Divide by 2. |
|
| Simplify. |
|
| Check: Let | |
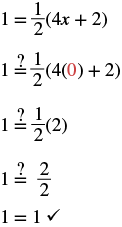 |
Many times, there will still be fractions, even after distributing.
Solve:
|
| |
| Distribute. |
|
| Simplify. |
|
| Multiply by the LCD, 4. |
|
| Distribute. |
|
| Simplify. |
|
| Collect the terms to the left. |
|
| Simplify. |
|
| Collect the constants to the right. |
|
| Simplify. |
|
| Check: Substitute for | |
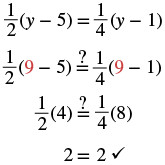 |
Some equations have decimals in them. This kind of equation will occur when we solve problems dealing with money and percent. But decimals are really another way to represent fractions. For example, and So, when we have an equation with decimals, we can use the same process we used to clear fractions—multiply both sides of the equation by the least common denominator .
Solve:
The only decimal in the equation is Since the LCD is We can multiply both sides by to clear the decimal.
|
| |
| Multiply both sides by the LCD. |
|
| Distribute. |
|
| Multiply, and notice, no more decimals! |
|
| Add 50 to get all constants to the right. |
|
| Simplify. |
|
| Divide both sides by 8. |
|
| Simplify. |
|
| Check: Let | |
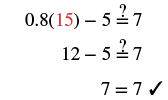 |
Solve:
Look at the decimals and think of the equivalent fractions.
Notice, the LCD is
By multiplying by the LCD we will clear the decimals.
|
| |
| Multiply both sides by 100. |
|
| Distribute. |
|
| Multiply, and now no more decimals. |
|
| Collect the variables to the right. |
|
| Simplify. |
|
| Collect the constants to the left. |
|
| Simplify. |
|
| Divide by 19. |
|
| Simplify. |
|
| Check: Let | |
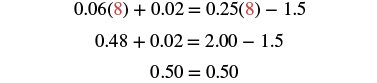 |
The next example uses an equation that is typical of the ones we will see in the money applications in the next chapter. Notice that we will distribute the decimal first before we clear all decimals in the equation.
Solve:
|
| |
| Distribute first. |
|
| Combine like terms. |
|
| To clear decimals, multiply by 100. |
|
| Distribute. |
|
| Subtract 15 from both sides. |
|
| Simplify. |
|
| Divide by 30. |
|
| Simplify. |
|
| Check: Let | |
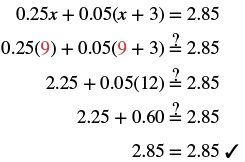 |

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?