| << Chapter < Page | Chapter >> Page > |
Because the Pythagorean Theorem contains variables that are squared, to solve for the length of a side in a right triangle, we will have to use square roots.
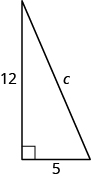
Use the Pythagorean Theorem to find the length of the hypotenuse shown below.
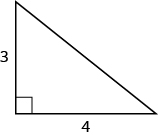
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | the length of the hypotenuse of the triangle |
|
Step 3. Name. Choose a variable to represent it.
Label side c on the figure. |
Let
c = the length of the hypotenuse.
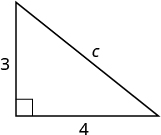 |
| Step 4. Translate. | |
| Write the appropriate formula. | |
| Substitute. | |
| Step 5. Solve the equation. | |
| Simplify. | |
| Use the definition of square root. | |
| Simplify. | |
Step 6. Check.
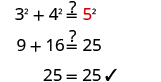 |
|
| Step 7. Answer the question. | The length of the hypotenuse is 5. |
Use the Pythagorean Theorem to find the length of the hypotenuse in the triangle shown below.
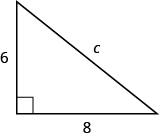
Use the Pythagorean Theorem to find the length of the hypotenuse in the triangle shown below.
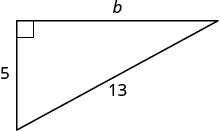
Use the Pythagorean Theorem to find the length of the leg shown below.

| Step 1. Read the problem. | ||
| Step 2. Identify what you are looking for. | the length of the leg of the triangle | |
| Step 3. Name. Choose a variable to represent it. | Let b = the leg of the triangle. | |
| Lable side b . |
 | |
| Step 4. Translate | ||
| Write the appropriate formula. | ||
| Substitute. | ||
| Step 5. Solve the equation. | ||
| Isolate the variable term. | ||
| Use the definition of square root. | ||
| Simplify. | ||
Step 6. Check.
 |
||
| Step 7. Answer the question. | The length of the leg is 12. |
Use the Pythagorean Theorem to find the length of the leg in the triangle shown below.
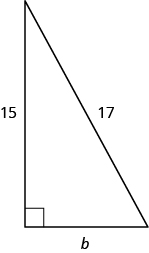
8
Use the Pythagorean Theorem to find the length of the leg in the triangle shown below.

12
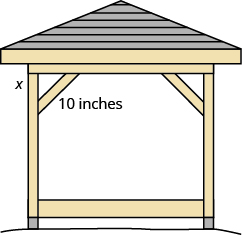
Kelvin is building a gazebo and wants to brace each corner by placing a piece of wood diagonally as shown above.
If he fastens the wood so that the ends of the brace are the same distance from the corner, what is the length of the legs of the right triangle formed? Approximate to the nearest tenth of an inch.
John puts the base of a 13-foot ladder five feet from the wall of his house as shown below. How far up the wall does the ladder reach?

12 feet
Randy wants to attach a 17 foot string of lights to the top of the 15 foot mast of his sailboat, as shown below. How far from the base of the mast should he attach the end of the light string?
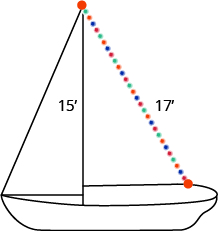
8 feet
You may already be familiar with the properties of rectangles. Rectangles have four sides and four right angles. The opposite sides of a rectangle are the same length. We refer to one side of the rectangle as the length, L , and its adjacent side as the width, W .

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?