| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
We solved some applications that are modeled by quadratic equations earlier, when the only method we had to solve them was factoring. Now that we have more methods to solve quadratic equations, we will take another look at applications. To get us started, we will copy our usual Problem Solving Strategy here so we can follow the steps.
We have solved number applications that involved consecutive even integers and consecutive odd integers by modeling the situation with linear equations. Remember, we noticed each even integer is 2 more than the number preceding it. If we call the first one n, then the next one is . The next one would be or . This is also true when we use odd integers. One set of even integers and one set of odd integers are shown below.
Some applications of consecutive odd integers or consecutive even integers are modeled by quadratic equations. The notation above will be helpful as you name the variables.
The product of two consecutive odd integers is 195. Find the integers.
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | We are looking for two consecutive odd integers. |
| Step 3. Name what we are looking for. | Let
the first odd integer.
the next odd integer |
| Step 4. Translate into an equation. State the problem in one sentence. | "The product of two consecutive odd integers is 195." The product of the first odd integer and the second odd integer is 195. |
| Translate into an equation |
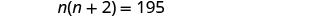 |
| Step 5. Solve the equation. Distribute. |
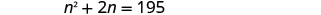 |
| Subtract 195 to get the equation in standard form. |
 |
| Identify the a, b, c values. |
 |
| Write the quadratic equation. |
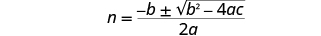 |
| Then substitute in the values of a, b, c. . |
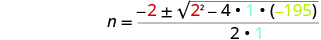 |
| Simplify. |
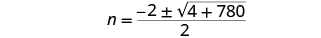
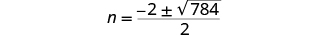 |
| Simplify the radical. |
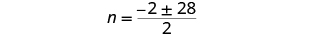 |
| Rewrite to show two solutions. |
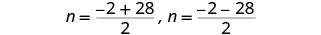 |
| Solve each equation. |
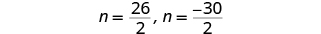
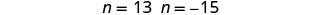 |
| There are two values of n that are solutions. This will give us two pairs of consecutive odd integers for our solution. | First odd integer
next odd integer |
| First odd integer
next odd integer | |
|
Step 6. Check the answer.
Do these pairs work? Are they consecutive odd integers? Is their product 195? |
|
| Step 7. Answer the question. | The two consecutive odd integers whose product is 195 are 13, 15, and −13, −15. |

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?