| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
We have solved systems of linear equations by graphing and by substitution. Graphing works well when the variable coefficients are small and the solution has integer values. Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression.
The third method of solving systems of linear equations is called the Elimination Method. When we solved a system by substitution, we started with two equations and two variables and reduced it to one equation with one variable. This is what we’ll do with the elimination method, too, but we’ll have a different way to get there.
The Elimination Method is based on the Addition Property of Equality. The Addition Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality. We will extend the Addition Property of Equality to say that when you add equal quantities to both sides of an equation, the results are equal.
For any expressions a , b , c , and d ,
To solve a system of equations by elimination, we start with both equations in standard form. Then we decide which variable will be easiest to eliminate. How do we decide? We want to have the coefficients of one variable be opposites, so that we can add the equations together and eliminate that variable.
Notice how that works when we add these two equations together:
The y ’s add to zero and we have one equation with one variable.
Let’s try another one:
This time we don’t see a variable that can be immediately eliminated if we add the equations.
But if we multiply the first equation by −2, we will make the coefficients of x opposites. We must multiply every term on both sides of the equation by −2.
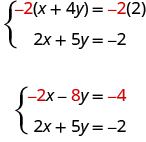
Now we see that the coefficients of the x terms are opposites, so x will be eliminated when we add these two equations.
Add the equations yourself—the result should be −3 y = −6. And that looks easy to solve, doesn’t it? Here is what it would look like.
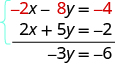
We’ll do one more:
It doesn’t appear that we can get the coefficients of one variable to be opposites by multiplying one of the equations by a constant, unless we use fractions. So instead, we’ll have to multiply both equations by a constant.
We can make the coefficients of x be opposites if we multiply the first equation by 3 and the second by −4, so we get 12 x and −12 x .

This gives us these two new equations:
When we add these equations,
the x ’s are eliminated and we just have −29 y = 58.

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?