| << Chapter < Page | Chapter >> Page > |
Translate the phrase into an algebraic expression: “the quotient of and
The keyword is quotient ; it tells us that the operation is division. Look for the words of and and to find the numbers to divide.
This tells us that we need to divide by
Translate the phrase into an algebraic expression: the quotient of and
Translate the phrase into an algebraic expression: the quotient of and
Translate the phrase into an algebraic expression: the quotient of the difference of and and
We are looking for the quotient of the difference of and , and This means we want to divide the difference of and by
Translate the phrase into an algebraic expression: the quotient of the difference of and and
Translate the phrase into an algebraic expression: the quotient of the sum of and and
Our work with fractions so far has included proper fractions, improper fractions, and mixed numbers. Another kind of fraction is called complex fraction , which is a fraction in which the numerator or the denominator contains a fraction.
Some examples of complex fractions are:
To simplify a complex fraction, remember that the fraction bar means division. So the complex fraction can be written as
Simplify:
| Rewrite as division. | |
| Multiply the first fraction by the reciprocal of the second. | |
| Multiply. | |
| Look for common factors. | |
| Remove common factors and simplify. |
Simplify:
| Rewrite as division. | |
| Multiply the first fraction by the reciprocal of the second. | |
| Multiply; the product will be negative. | |
| Look for common factors. | |
| Remove common factors and simplify. |
Simplify:
| Rewrite as division. | |
| Multiply the first fraction by the reciprocal of the second. | |
| Multiply. | |
| Look for common factors. | |
| Remove common factors and simplify. |
Simplify:
| Rewrite as division. | |
| Change the mixed number to an improper fraction. | |
| Multiply the first fraction by the reciprocal of the second. | |
| Multiply. | |
| Look for common factors. | |
| Remove common factors and simplify. |
Where does the negative sign go in a fraction? Usually, the negative sign is placed in front of the fraction, but you will sometimes see a fraction with a negative numerator or denominator. Remember that fractions represent division. The fraction could be the result of dividing a negative by a positive, or of dividing a positive by a negative. When the numerator and denominator have different signs, the quotient is negative.
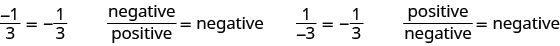
If both the numerator and denominator are negative, then the fraction itself is positive because we are dividing a negative by a negative.

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?