| << Chapter < Page | Chapter >> Page > |
Simplify:
| Use the Power of a Product Property. | |
| Use the Power Property. | |
| Use the Commutative Property. | |
| Multiply the constants and add the exponents for
each variable. |
Since a monomial is an algebraic expression, we can use the properties for simplifying expressions with exponents to multiply the monomials.
Multiply:
| Use the Commutative Property to rearrange the factors. | |
| Multiply. |
Multiply:
| Use the Commutative Property to rearrange
the factors. |
|
| Multiply. |
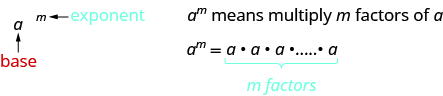
This is read to the power.
Simplify Expressions with Exponents
In the following exercises, simplify each expression with exponents.
Simplify Expressions Using the Product Property of Exponents
In the following exercises, simplify each expression using the Product Property of Exponents.
Simplify Expressions Using the Power Property of Exponents
In the following exercises, simplify each expression using the Power Property of Exponents .
Simplify Expressions Using the Product to a Power Property
In the following exercises, simplify each expression using the Product to a Power Property.
Simplify Expressions by Applying Several Properties
In the following exercises, simplify each expression.
Multiply Monomials
In the following exercises, multiply the following monomials.
Email Janet emails a joke to six of her friends and tells them to forward it to six of their friends, who forward it to six of their friends, and so on. The number of people who receive the email on the second round is on the third round is as shown in the table. How many people will receive the email on the eighth round? Simplify the expression to show the number of people who receive the email.
| Round | Number of people |
|---|---|
1,679,616
Salary Raul’s boss gives him a raise every year on his birthday. This means that each year, Raul’s salary is times his last year’s salary. If his original salary was , his salary after year was after years was after years was as shown in the table below. What will Raul’s salary be after years? Simplify the expression, to show Raul’s salary in dollars.
| Year | Salary |
|---|---|
Use the Product Property for Exponents to explain why
Answers will vary.
Explain why but
Jorge thinks is What is wrong with his reasoning?
Answers will vary.
Explain why is and not
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?