| << Chapter < Page | Chapter >> Page > |
Use the Definition of a Negative Exponent
In the following exercises, simplify.
Simplify Expressions with Integer Exponents
In the following exercises, simplify .
Convert from Decimal Notation to Scientific Notation
In the following exercises, write each number in scientific notation.
8,750,000
0.00000924
The population of the United States on July 4, 2010 was almost
The population of the world on July 4, 2010 was more than
6.85 × 10 9
The average width of a human hair is centimeters.
The probability of winning the Megamillions lottery is about
5.7 × 10 −9
Convert Scientific Notation to Decimal Form
In the following exercises, convert each number to decimal form.
In 2010, the number of Facebook users each day who changed their status to ‘engaged’ was
At the start of 2012, the US federal budget had a deficit of more than
$15,000,000,000,000
The concentration of carbon dioxide in the atmosphere is
Multiply and Divide Using Scientific Notation
In the following exercises, multiply or divide and write your answer in decimal form.
Calories In May 2010 the Food and Beverage Manufacturers pledged to reduce their products by trillion calories by the end of 2015.
Length of a year The difference between the calendar year and the astronomical year is day.
Calculator display Many calculators automatically show answers in scientific notation if there are more digits than can fit in the calculator’s display. To find the probability of getting a particular 5-card hand from a deck of cards, Mario divided by and saw the answer Write the number in decimal notation.
Calculator display Many calculators automatically show answers in scientific notation if there are more digits than can fit in the calculator’s display. To find the number of ways Barbara could make a collage with of her favorite photographs, she multiplied Her calculator gave the answer Write the number in decimal notation.
11,441,304,000
When you convert a number from decimal notation to scientific notation, how do you know if the exponent will be positive or negative?
Answers will vary.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
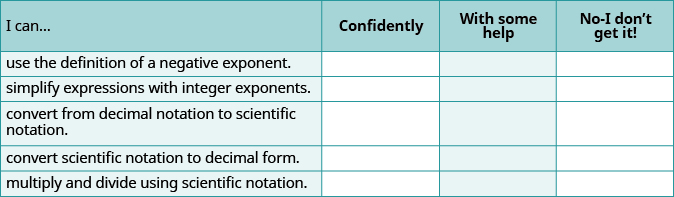
ⓑ After looking at the checklist, do you think you are well prepared for the next section? Why or why not?

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?