| << Chapter < Page | Chapter >> Page > |
We’ll work one now where the middle term is negative.
Factor: .
The first and last terms are squares. See if the middle term fits the pattern of a perfect square trinomial. The middle term is negative, so the binomial square would be .
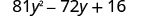 | |
| Are the first and last terms perfect squares? |
 |
| Check the middle term. |
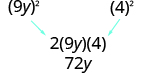 |
| Does is match ? Yes. |
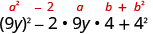 |
| Write the square of a binomial. |
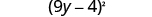 |
| Check by mulitplying. | |
The next example will be a perfect square trinomial with two variables.
Factor: .
 | |
| Test each term to verify the pattern. |
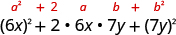 |
| Factor. |
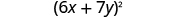 |
| Check by mulitplying. | |
Remember the very first step in our Strategy for Factoring Polynomials? It was to ask “is there a greatest common factor?” and, if there was, you factor the GCF before going any further. Perfect square trinomials may have a GCF in all three terms and it should be factored out first. And, sometimes, once the GCF has been factored, you will recognize a perfect square trinomial.
Factor: .
| Is there a GCF? Yes, 4 y , so factor it out. | |
| Is this a perfect square trinomial? | |
| Verify the pattern. |
 |
| Factor. | |
| Remember: Keep the factor 4 y in the final product. | |
| Check. | |
The other special product you saw in the previous was the Product of Conjugates pattern. You used this to multiply two binomials that were conjugates. Here’s an example:
Remember, when you multiply conjugate binomials, the middle terms of the product add to 0. All you have left is a binomial, the difference of squares.
Multiplying conjugates is the only way to get a binomial from the product of two binomials.
If a and b are real numbers
The product is called a difference of squares.
To factor, we will use the product pattern “in reverse” to factor the difference of squares. A difference of squares factors to a product of conjugates.
If a and b are real numbers,

Remember, “difference” refers to subtraction. So, to use this pattern you must make sure you have a binomial in which two squares are being subtracted.

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?