| << Chapter < Page | Chapter >> Page > |
The sum of two numbers is 39. Their difference is 9. Find the numbers.
The sum of two numbers is 42. Their difference is 8. Find the numbers.
The numbers are 25 and 17.
The sum of two numbers is −15. Their difference is −35. Find the numbers.
The numbers are −25 and 10.
Joe stops at a burger restaurant every day on his way to work. Monday he had one order of medium fries and two small sodas, which had a total of 620 calories. Tuesday he had two orders of medium fries and one small soda, for a total of 820 calories. How many calories are there in one order of medium fries? How many calories in one small soda?
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | We are looking for the number of
calories in one order of medium fries and in one small soda. |
| Step 3. Name what we are looking for. | Let
f = the number of calories in
1 order of medium fries. s = the number of calories in 1 small soda. |
| Step 4. Translate into a system of equations: | one medium fries and two small sodas had a
total of 620 calories |
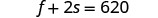 | |
| two medium fries and one small soda had a
total of 820 calories. | |
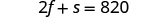 | |
| Our system is: |
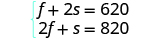 |
|
Step 5. Solve the system of equations.
To solve the system of equations, use elimination. The equations are in standard form. To get opposite coefficients of f , multiply the top equation by −2. |
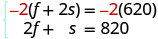 |
| Simplify and add. |
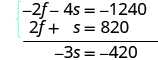 |
| Solve for s . |
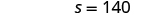 |
| Substitute
s = 140 into one of the original
equations and then solve for f . |
 |
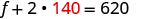 | |
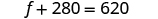 | |
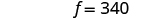 | |
| Step 6. Check the answer. | Verify that these numbers make sense
in the problem and that they are solutions to both equations. We leave this to you! |
| Step 7. Answer the question. | The small soda has 140 calories and
the fries have 340 calories. |
Malik stops at the grocery store to buy a bag of diapers and 2 cans of formula. He spends a total of $37. The next week he stops and buys 2 bags of diapers and 5 cans of formula for a total of $87. How much does a bag of diapers cost? How much is one can of formula?
The bag of diapers costs $11 and the can of formula costs $13.
To get her daily intake of fruit for the day, Sasha eats a banana and 8 strawberries on Wednesday for a calorie count of 145. On the following Wednesday, she eats two bananas and 5 strawberries for a total of 235 calories for the fruit. How many calories are there in a banana? How many calories are in a strawberry?
There are 105 calories in a banana and 5 calories in a strawberry.

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?