| << Chapter < Page | Chapter >> Page > |
Look back at the equations in [link] . Is there any way to recognize that they are the same line?
Let’s see what happens in the next example.
Solve the system by substitution.
The second equation is already solved for y , so we can substitute for y in the first equation.
| Substitute x for y in the first equation. |
 |
| Replace the y with |
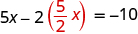 |
| Solve for x . |
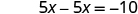 |
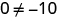 |
Since 0 = −10 is a false statement the equations are inconsistent. The graphs of the two equation would be parallel lines. The system has no solutions.
We’ll copy here the problem solving strategy we used in the Solving Systems of Equations by Graphing section for solving systems of equations. Now that we know how to solve systems by substitution, that’s what we’ll do in Step 5.
Some people find setting up word problems with two variables easier than setting them up with just one variable. Choosing the variable names is easier when all you need to do is write down two letters. Think about this in the next example—how would you have done it with just one variable?
The sum of two numbers is zero. One number is nine less than the other. Find the numbers.
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | We are looking for two numbers. |
| Step 3. Name what we are looking for. | Let
the first number
Let the second number |
| Step 4. Translate into a system of equations. | The sum of two numbers is zero. |
 | |
| One number is nine less than the other. | |
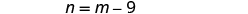 | |
| The system is: |
 |
|
Step 5. Solve the system of
equations. We will use substitution since the second equation is solved for n . |
|
| Substitute m − 9 for n in the first equation. |
 |
| Solve for m . |
 |
 | |
 | |
| Substitute
into the second equation
and then solve for n . |
 |
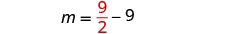 | |
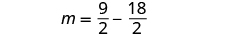 | |
 | |
| Step 6. Check the answer in the problem. | Do these numbers make sense in
the problem? We will leave this to you! |
| Step 7. Answer the question. | The numbers are and |
The sum of two numbers is 10. One number is 4 less than the other. Find the numbers.
The numbers are 3 and 7.
The sum of two number is −6. One number is 10 less than the other. Find the numbers.
The numbers are 2 and −8.
In the [link] , we’ll use the formula for the perimeter of a rectangle, P = 2 L + 2 W .
The perimeter of a rectangle is 88. The length is five more than twice the width. Find the length and the width.
| Step 1. Read the problem. |
 |
| Step 2. Identify what you are looking for. | We are looking for the length and width. |
| Step 3. Name what we are looking for. | Let
the length
the width |
| Step 4. Translate into a system of equations. | The perimeter of a rectangle is 88. |
2
L + 2
W =
P
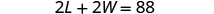 | |
| The length is five more than twice the width. | |
 | |
| The system is: |
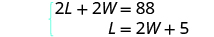 |
|
Step 5. Solve the system of equations.
We will use substitution since the second equation is solved for L . Substitute 2 W + 5 for L in the first equation. |
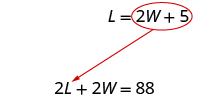 |
| Solve for W . |
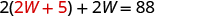 |
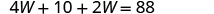 | |
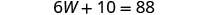 | |
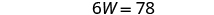 | |
| Substitute
W = 13 into the second
equation and then solve for L . |
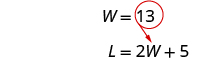 |
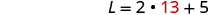 | |
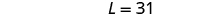 | |
| Step 6. Check the answer in the problem. | Does a rectangle with length 31 and width
13 have perimeter 88? Yes. |
| Step 7. Answer the equation. | The length is 31 and the width is 13. |

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?