| << Chapter < Page | Chapter >> Page > |
Thanh and Nhat leave their office in Sacramento at the same time. Thanh drives north on I-5 at a speed of 72 miles per hour. Nhat drives south on I-5 at a speed of 76 miles per hour. How long will it take them to be 330 miles apart?
2.2 hours
It is important to make sure the units match when we use the distance rate and time formula. For instance, if the rate is in miles per hour, then the time must be in hours.
When Katie Mae walks to school, it takes her 30 minutes. If she rides her bike, it takes her 15 minutes. Her speed is three miles per hour faster when she rides her bike than when she walks. What are her walking speed and her speed riding her bike?
First, we draw a diagram that represents the situation to help us see what is happening.
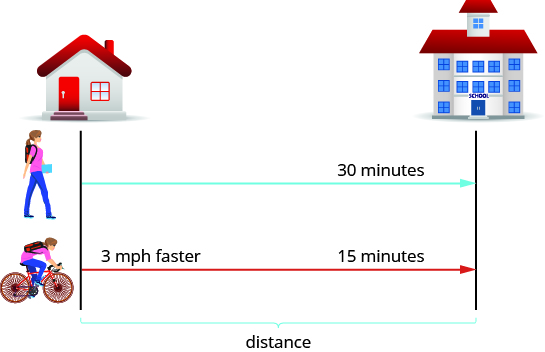
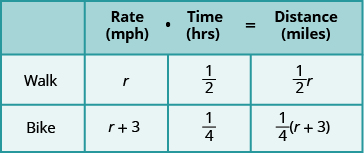
We are asked to find her speed walking and riding her bike. Let’s call her walking speed r . Since her biking speed is three miles per hour faster, we will call that speed We write the speeds in the chart.
The speed is in miles per hour, so we need to express the times in hours, too, in order for the units to be the same. Remember, one hour is 60 minutes. So:
Next, we multiply rate times time to fill in the distance column.
The equation will come from the fact that the distance from Katie Mae’s home to her school is the same whether she is walking or riding her bike.
So we say:
 | |
| Translate into an equation. |
 |
| Solve this equation. |
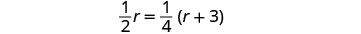 |
| Clear the fractions by multiplying by the LCD of all the fractions in the equation. |
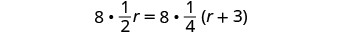 |
| Simplify. |
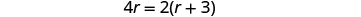
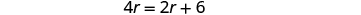


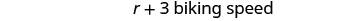

6 mph (Katie Mae's biking speed) |
| Let's check if this works.
Walk 3 mph (0.5 hour) = 1.5 miles Bike 6 mph (0.25 hour) = 1.5 miles |
|
| Yes, either way Katie Mae travels 1.5 miles to school. | Katie Mae’s walking speed is 3 mph.
Her speed riding her bike is 6 mph. |
Suzy takes 50 minutes to hike uphill from the parking lot to the lookout tower. It takes her 30 minutes to hike back down to the parking lot. Her speed going downhill is 1.2 miles per hour faster than her speed going uphill. Find Suzy’s uphill and downhill speeds.
uphill 1.8 mph, downhill three mph
Llewyn takes 45 minutes to drive his boat upstream from the dock to his favorite fishing spot. It takes him 30 minutes to drive the boat back downstream to the dock. The boat’s speed going downstream is four miles per hour faster than its speed going upstream. Find the boat’s upstream and downstream speeds.
upstream 8 mph, downstream 12 mph
In the distance, rate, and time formula, time represents the actual amount of elapsed time (in hours, minutes, etc.). If a problem gives us starting and ending times as clock times, we must find the elapsed time in order to use the formula.
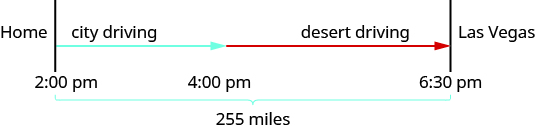
Hamilton loves to travel to Las Vegas, 255 miles from his home in Orange County. On his last trip, he left his house at 2:00 pm. The first part of his trip was on congested city freeways. At 4:00 pm, the traffic cleared and he was able to drive through the desert at a speed 1.75 times faster than when he drove in the congested area. He arrived in Las Vegas at 6:30 pm. How fast was he driving during each part of his trip?
A diagram will help us model this trip.
Next, we create a table to organize the information.
We know the total distance is 255 miles. We are looking for the rate of speed for each part of the trip. The rate in the desert is 1.75 times the rate in the city. If we let the rate in the city, then the rate in the desert is
The times here are given as clock times. Hamilton started from home at 2:00 pm and entered the desert at 4:30 pm. So he spent two hours driving the congested freeways in the city. Then he drove faster from 4:00 pm until 6:30 pm in the desert. So he drove 2.5 hours in the desert.
Now, we multiply the rates by the times.
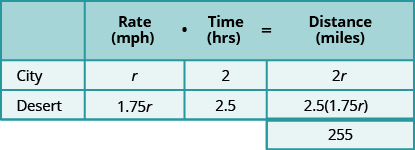
By looking at the diagram below, we can see that the sum of the distance driven in the city and the distance driven in the desert is 255 miles.
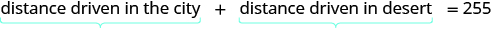 | |
| Translate into an equation. |
 |
| Solve this equation. |
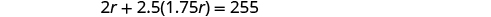
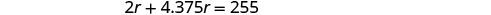
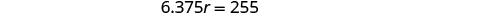
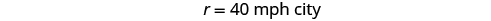
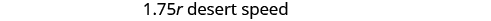
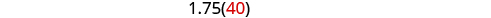
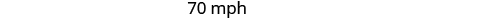 |
Check.

|
|
| Hamilton drove 40 mph in the city and 70 mph in the desert. |

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?