| << Chapter < Page | Chapter >> Page > |
Wayne and Dennis like to ride the bike path from Riverside Park to the beach. Dennis’s speed is seven miles per hour faster than Wayne’s speed, so it takes Wayne 2 hours to ride to the beach while it takes Dennis 1.5 hours for the ride. Find the speed of both bikers.
Wayne 21 mph, Dennis 28 mph
Jeromy can drive from his house in Cleveland to his college in Chicago in 4.5 hours. It takes his mother 6 hours to make the same drive. Jeromy drives 20 miles per hour faster than his mother. Find Jeromy’s speed and his mother’s speed.
Jeromy 80 mph, mother 60 mph
In [link] , the last example, we had two trains traveling the same distance. The diagram and the chart helped us write the equation we solved. Let’s see how this works in another case.
Christopher and his parents live 115 miles apart. They met at a restaurant between their homes to celebrate his mother’s birthday. Christopher drove 1.5 hours while his parents drove 1 hour to get to the restaurant. Christopher’s average speed was 10 miles per hour faster than his parents’ average speed. What were the average speeds of Christopher and of his parents as they drove to the restaurant?
Step 1. Read the problem. Make sure all the words and ideas are understood.
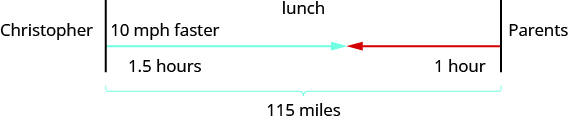
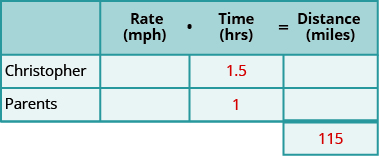
Step 2. Identify what we are looking for.
Step 3. Name what we are looking for. Choose a variable to represent that quantity.
Fill in the speeds into the chart.
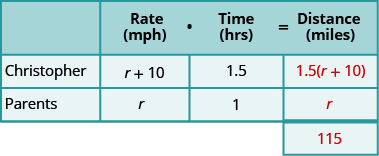
Multiply the rate times the time to get the distance.
Step 4. Translate into an equation.
The distance Christopher travelled plus the distance his parents travel must add up to 115 miles. So we write:
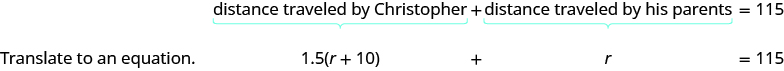
Step 5. Solve the equation using good algebra techniques.
Step 6. Check the answer in the problem and make sure it makes sense.

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?