| << Chapter < Page | Chapter >> Page > |
Use the formula to find the principal, :
ⓐ when ⓑ in general
ⓐ $9,000 ⓑ
Later in this class, and in future algebra classes, you’ll encounter equations that relate two variables, usually x and y . You might be given an equation that is solved for y and need to solve it for x , or vice versa. In the following example, we’re given an equation with both x and y on the same side and we’ll solve it for y .
Solve the formula for y :
ⓐ when ⓑ in general
| ⓐ when | ⓑ in general | ||||
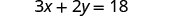 |
 | ||||
| Substitute. |
 |
||||
| Subtract to isolate the
-term. |
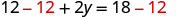 |
Subtract to isolate the
-term. |
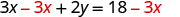 | ||
| Divide. |
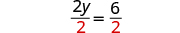 |
Divide. |
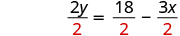 | ||
| Simplify. |
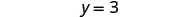 |
Simplify. |
 |
In Examples 1.60 through 1.64 we used the numbers in part ⓐ as a guide to solving in general in part ⓑ . Now we will solve a formula in general without using numbers as a guide.
Solve the formula for .
| We will isolate on one side of the equation. |
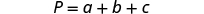 |
| Both and are added to , so we subtract them from both sides of the equation. |
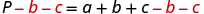 |
| Simplify. |

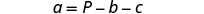 |
Solve the formula for y.
 | |
| Subtract from both sides to isolate the term with . |
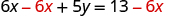 |
| Simplify. |
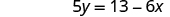 |
| Divide by 5 to make the coefficient 1. |
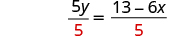 |
| Simplify. |
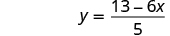 |
The fraction is simplified. We cannot divide by 5.
Use the Distance, Rate, and Time Formula
In the following exercises, solve.
Steve drove for hours at 72 miles per hour. How much distance did he travel?
Socorro drove for hours at 60 miles per hour. How much distance did she travel?
290 miles
Yuki walked for hours at 4 miles per hour. How far did she walk?
Francie rode her bike for hours at 12 miles per hour. How far did she ride?
30 miles
Connor wants to drive from Tucson to the Grand Canyon, a distance of 338 miles. If he drives at a steady rate of 52 miles per hour, how many hours will the trip take?
Megan is taking the bus from New York City to Montreal. The distance is 380 miles and the bus travels at a steady rate of 76 miles per hour. How long will the bus ride be?
5 hours

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?