| << Chapter < Page | Chapter >> Page > |
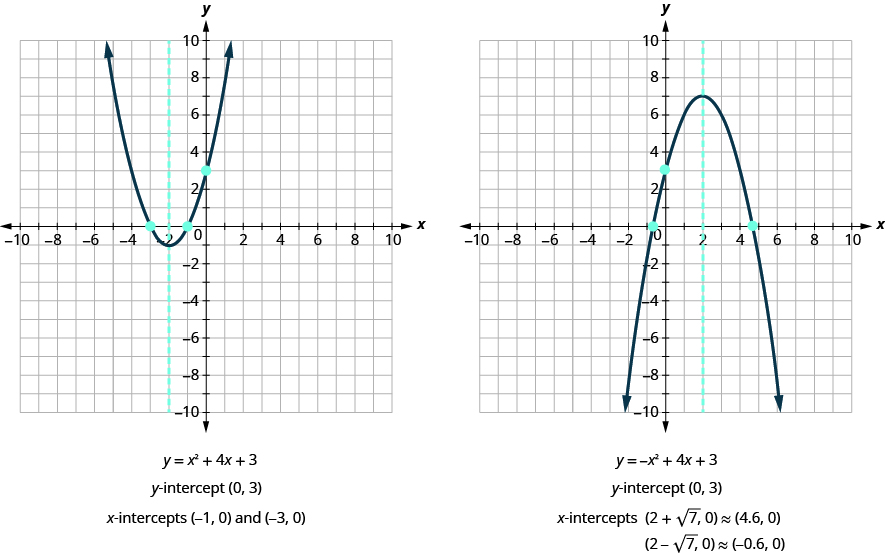
Do these results agree with our graphs? See [link] .
To find the intercepts of a parabola with equation :
Find the intercepts of the parabola .
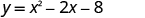 | |
| To find the y -intercept, let and solve for y . |
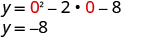 |
| When
, then
.
The y -intercept is the point . | |
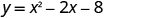 | |
| To find the x -intercept, let and solve for x . |
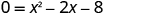 |
| Solve by factoring. |
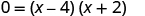 |
 |
When , then . The x -intercepts are the points and .
In this chapter, we have been solving quadratic equations of the form . We solved for and the results were the solutions to the equation.
We are now looking at quadratic equations in two variables of the form . The graphs of these equations are parabolas. The x -intercepts of the parabolas occur where .
For example:
The solutions of the quadratic equation are the values of the x -intercepts.
Earlier, we saw that quadratic equations have 2, 1, or 0 solutions. The graphs below show examples of parabolas for these three cases. Since the solutions of the equations give the x -intercepts of the graphs, the number of x -intercepts is the same as the number of solutions.
Previously, we used the discriminant to determine the number of solutions of a quadratic equation of the form . Now, we can use the discriminant to tell us how many x -intercepts there are on the graph.
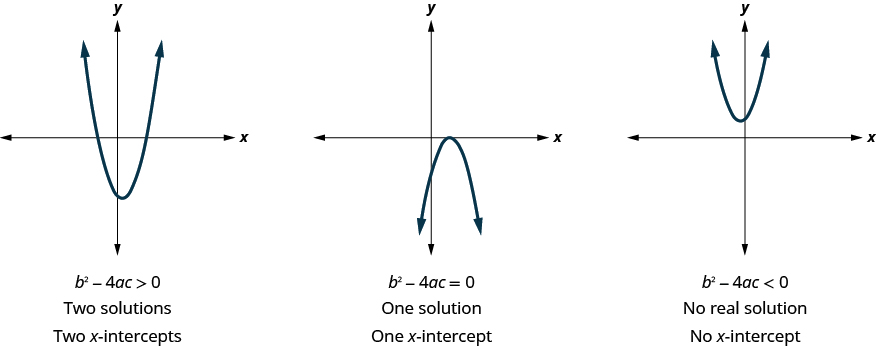
Before you start solving the quadratic equation to find the values of the x -intercepts, you may want to evaluate the discriminant so you know how many solutions to expect.
Find the intercepts of the parabola .
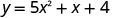 | |
| To find the y -intercept, let and solve for y . |
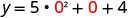

When , then . The y -intercept is the point . |
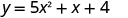 | |
| To find the x -intercept, let and solve for x . |
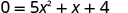 |
| Find the value of the discriminant to predict the number of solutions and so x -intercepts. | |
| Since the value of the discriminant is negative, there is no real solution to the equation. | There are no x -intercepts. |
Find the intercepts of the parabola .
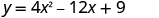 | |
| To find the y -intercept, let and solve for y . |
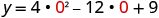
 |
| When
, then
.
The y -intercept is the point . | |
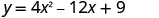 | |
| To find the x -intercept, let and solve for x . |
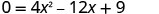 |
| Find the value of the discriminant to predict the number of solutions and so x -intercepts. | |
| Since the value of the discriminant is 0, there is no real solution to the equation. So there is one x -intercept. | |
| Solve the equation by factoring the perfect square trinomial. |
 |
| Use the Zero Product Property. |
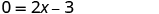 |
| Solve for x . |

 |
| When , then | |
| The x -intercept is the point |

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?