| << Chapter < Page | Chapter >> Page > |
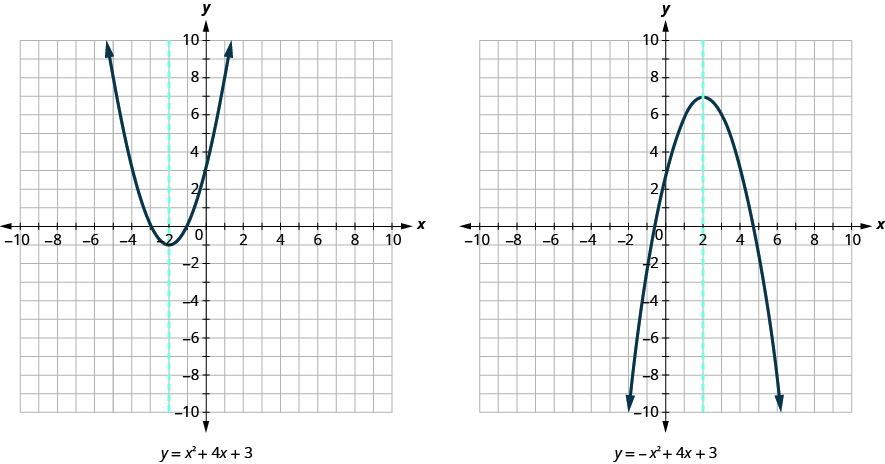
We show the same two graphs again with the axis of symmetry in red. See [link] .
The equation of the axis of symmetry can be derived by using the Quadratic Formula. We will omit the derivation here and proceed directly to using the result. The equation of the axis of symmetry of the graph of is
So, to find the equation of symmetry of each of the parabolas we graphed above, we will substitute into the formula .
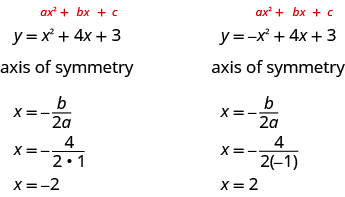
Look back at [link] . Are these the equations of the dashed red lines?
The point on the parabola that is on the axis of symmetry is the lowest or highest point on the parabola, depending on whether the parabola opens upwards or downwards. This point is called the vertex of the parabola.
We can easily find the coordinates of the vertex, because we know it is on the axis of symmetry. This means its x -coordinate is . To find the y -coordinate of the vertex, we substitute the value of the x -coordinate into the quadratic equation.
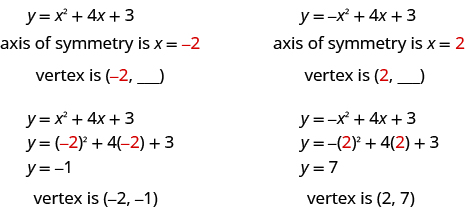
For a parabola with equation :
To find the y -coordinate of the vertex, we substitute into the quadratic equation.
For the parabola find: ⓐ the axis of symmetry and ⓑ the vertex.
| ⓐ |
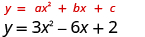 |
| The axis of symmetry is the line . |
 |
| Substitute the values of a, b into the equation. |
 |
| Simplify. | |
| The axis of symmetry is the line . | |
| ⓑ |
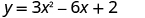 |
| The vertex is on the line of symmetry, so its x -coordinate will be . | |
| Substitute into the equation and solve for y. |
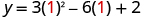 |
| Simplify. |
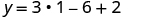 |
| This is the y -coordinate. |
The vertex is |
For the parabola find: ⓐ the axis of symmetry and ⓑ the vertex.
ⓐ ⓑ
For the parabola find: ⓐ the axis of symmetry and ⓑ the vertex.
ⓐ ⓑ
When we graphed linear equations, we often used the x - and y -intercepts to help us graph the lines. Finding the coordinates of the intercepts will help us to graph parabolas, too.
Remember, at the y -intercept the value of is zero. So, to find the y -intercept, we substitute into the equation.
Let’s find the y -intercepts of the two parabolas shown in the figure below.
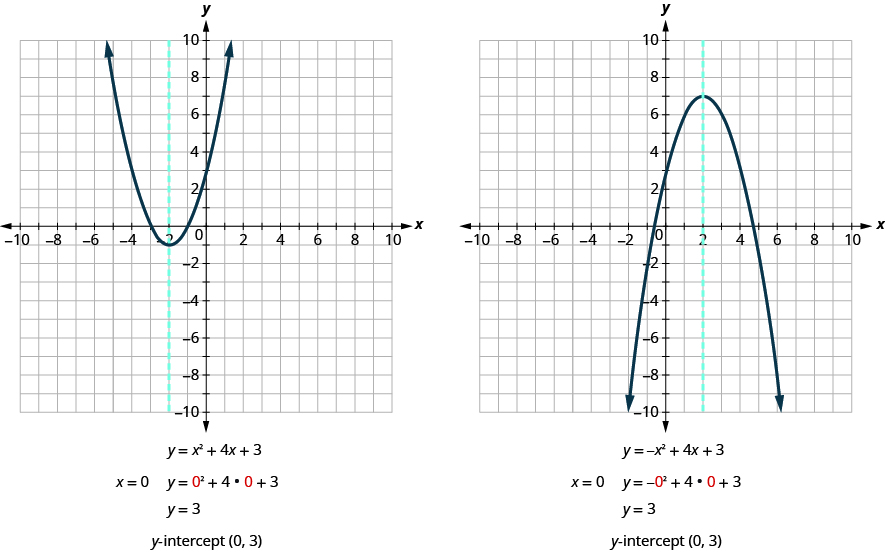
At an x -intercept , the value of is zero. To find an x -intercept, we substitute into the equation. In other words, we will need to solve the equation for .
But solving quadratic equations like this is exactly what we have done earlier in this chapter.
We can now find the x -intercepts of the two parabolas shown in [link] .
First, we will find the x -intercepts of a parabola with equation .
 | |
| Let . |
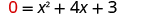 |
| Factor. |
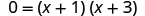 |
| Use the zero product property. |
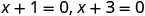 |
| Solve. |
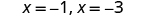 |
| The x intercepts are and |
Now, we will find the x -intercepts of the parabola with equation .
 | |
| Let . |
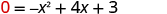 |
| This quadratic does not factor, so we use the Quadratic Formula. |
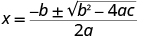 |
| , , |
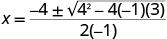 |
| Simplify. |
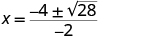
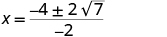
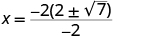
 |
| The x intercepts are and . |
We will use the decimal approximations of the x-intercepts, so that we can locate these points on the graph.

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?