| << Chapter < Page | Chapter >> Page > |
In each case we got 8—either 8 positives or 8 negatives.
When the signs were the same, the counters were all the same color, and so we added them.

Add: ⓐ ⓑ
ⓐ
 |
| 1 positive plus 4 positives is 5 positives. |
ⓑ
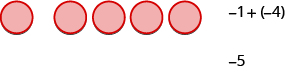 |
| 1 negative plus 4 negatives is 5 negatives. |
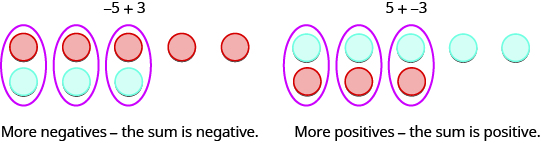
So what happens when the signs are different? Let’s add We realize this means the sum of and 3. When the counters were the same color, we put them in a row. When the counters are a different color, we line them up under each other.
| −5 + 3 means the sum of −5 and 3. | |
| We start with 5 negatives. |
 |
| And then we add 3 positives. |
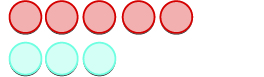 |
| We remove any neutral pairs. |
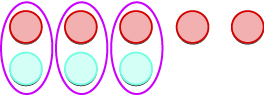 |
| We have 2 negatives left. |
 |
| The sum of −5 and 3 is −2. | −5 + 3 = −2 |
Notice that there were more negatives than positives, so the result was negative.
Let’s now add the last combination,
| 5 + (−3) means the sum of 5 and −3. | |
| We start with 5 positives. |
 |
| And then we add 3 negatives. |
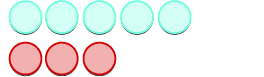 |
| We remove any neutral pairs. |
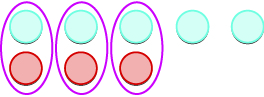 |
| We have 2 positives left. |
 |
| The sum of 5 and −3 is 2. | 5 + (−3) = 2 |
When we use counters to model addition of positive and negative integers, it is easy to see whether there are more positive or more negative counters. So we know whether the sum will be positive or negative.
Add: ⓐ ⓑ
ⓐ
| −1 + 5 | |
 | |
| There are more positives, so the sum is positive. | 4 |
| 1 + (−5) | |
 | |
| There are more negatives, so the sum is negative. | −4 |
Now that we have added small positive and negative integers with a model, we can visualize the model in our minds to simplify problems with any numbers.
When you need to add numbers such as you really don’t want to have to count out 37 blue counters and 53 red counters. With the model in your mind, can you visualize what you would do to solve the problem?
Picture 37 blue counters with 53 red counters lined up underneath. Since there would be more red (negative) counters than blue (positive) counters, the sum would be negative . How many more red counters would there be? Because there are 16 more red counters.
Therefore, the sum of is
Let’s try another one. We’ll add Again, imagine 74 red counters and 27 more red counters, so we’d have 101 red counters. This means the sum is
Let’s look again at the results of adding the different combinations of and
When the signs are the same, the counters would be all the same color, so add them.
When the signs are different, some of the counters would make neutral pairs, so subtract to see how many are left.
Visualize the model as you simplify the expressions in the following examples.
Simplify: ⓐ ⓑ

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?