| << Chapter < Page | Chapter >> Page > |
Determine if each is an expression or an equation: ⓐ ⓑ .
ⓐ equation ⓑ expression
Determine if each is an expression or an equation: ⓐ ⓑ .
ⓐ expression ⓑ equation
Suppose we need to multiply 2 nine times. We could write this as This is tedious and it can be hard to keep track of all those 2s, so we use exponents. We write as and as In expressions such as the 2 is called the base and the 3 is called the exponent . The exponent tells us how many times we need to multiply the base.
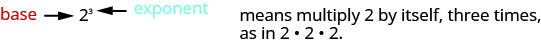
We read as “two to the third power” or “two cubed.”
We say is in exponential notation and is in expanded notation .
means multiply a by itself, n times.

The expression is read a to the power.
While we read as “ a to the power,” we usually read:
We’ll see later why and have special names.
[link] shows how we read some expressions with exponents.
| Expression | In Words |
|---|---|
| 7 to the second power or 7 squared | |
| 5 to the third power or 5 cubed | |
| 9 to the fourth power | |
| to the fifth power |
To simplify an expression means to do all the math possible. For example, to simplify we’d first multiply to get 8 and then add the 1 to get 9. A good habit to develop is to work down the page, writing each step of the process below the previous step. The example just described would look like this:
By not using an equal sign when you simplify an expression, you may avoid confusing expressions with equations.
To simplify an expression , do all operations in the expression.
We’ve introduced most of the symbols and notation used in algebra, but now we need to clarify the order of operations. Otherwise, expressions may have different meanings, and they may result in different values. For example, consider the expression:
If you simplify this expression, what do you get?
Some students say 49,
Others say 25,
Imagine the confusion in our banking system if every problem had several different correct answers!
The same expression should give the same result. So mathematicians early on established some guidelines that are called the Order of Operations .

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?