| << Chapter < Page | Chapter >> Page > |
The revenue in millions of dollars for a fictional cable company from 2006 through 2013 is shown in [link] .
| Year | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| Revenues | 52.4 | 52.8 | 51.2 | 49.5 | 48.6 | 48.6 | 48.7 | 47.1 |
The revenue can be modeled by the polynomial function
where represents the revenue in millions of dollars and represents the year, with corresponding to 2006. Over which intervals is the revenue for the company increasing? Over which intervals is the revenue for the company decreasing? These questions, along with many others, can be answered by examining the graph of the polynomial function. We have already explored the local behavior of quadratics, a special case of polynomials. In this section we will explore the local behavior of polynomials in general.
Polynomial functions of degree 2 or more have graphs that do not have sharp corners; recall that these types of graphs are called smooth curves. Polynomial functions also display graphs that have no breaks. Curves with no breaks are called continuous. [link] shows a graph that represents a polynomial function and a graph that represents a function that is not a polynomial.
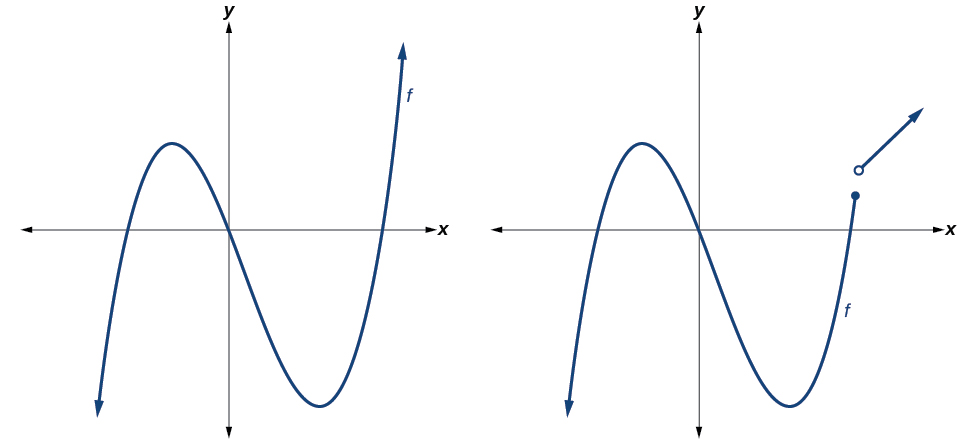
The graphs of and are graphs of polynomial functions. They are smooth and continuous .
The graphs of and are graphs of functions that are not polynomials. The graph of function has a sharp corner. The graph of function is not continuous.
Do all polynomial functions have as their domain all real numbers?
Yes. Any real number is a valid input for a polynomial function.
Recall that if is a polynomial function, the values of for which are called zeros of If the equation of the polynomial function can be factored, we can set each factor equal to zero and solve for the zeros .
We can use this method to find intercepts because at the intercepts we find the input values when the output value is zero. For general polynomials, this can be a challenging prospect. While quadratics can be solved using the relatively simple quadratic formula, the corresponding formulas for cubic and fourth-degree polynomials are not simple enough to remember, and formulas do not exist for general higher-degree polynomials. Consequently, we will limit ourselves to three cases in this section:
Given a polynomial function find the x -intercepts by factoring.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?