| << Chapter < Page | Chapter >> Page > |
What might a scatterplot of data points look like if it were best described by a logarithmic model?
What does the y -intercept on the graph of a logistic equation correspond to for a population modeled by that equation?
The y -intercept on the graph of a logistic equation corresponds to the initial population for the population model.
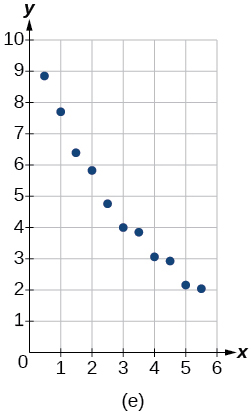
For the following exercises, match the given function of best fit with the appropriate scatterplot in [link] through [link] . Answer using the letter beneath the matching graph.
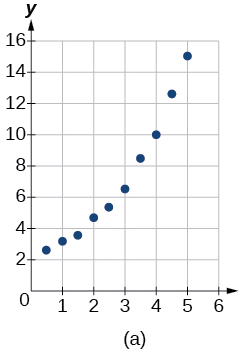
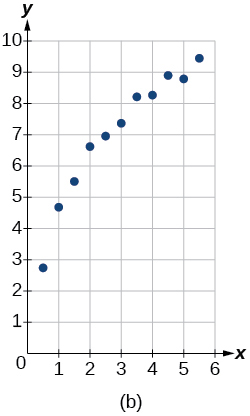
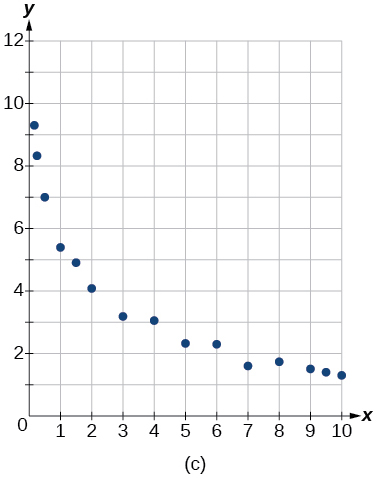
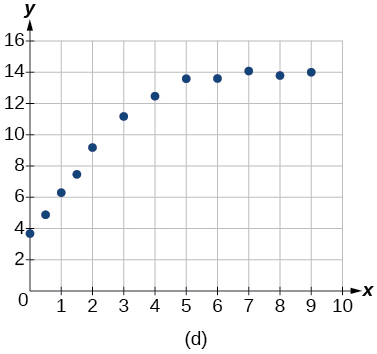
To the nearest whole number, what is the initial value of a population modeled by the logistic equation What is the carrying capacity?
; 175
Rewrite the exponential model as an equivalent model with base Express the exponent to four significant digits.
A logarithmic model is given by the equation To the nearest hundredth, for what value of does
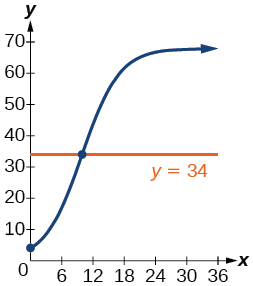
A logistic model is given by the equation To the nearest hundredth, for what value of t does
What is the y -intercept on the graph of the logistic model given in the previous exercise?
y -intercept:
For the following exercises, use this scenario: The population of a koi pond over months is modeled by the function
Graph the population model to show the population over a span of years.
How many koi will the pond have after one and a half years?
How many months will it take before there are koi in the pond?
about months.
Use the intersect feature to approximate the number of months it will take before the population of the pond reaches half its carrying capacity.
For the following exercises, use this scenario: The population of an endangered species habitat for wolves is modeled by the function where is given in years.
Graph the population model to show the population over a span of years.
What was the initial population of wolves transported to the habitat?
wolves
How many wolves will the habitat have after years?
How many years will it take before there are wolves in the habitat?
about 5.4 years.
Use the intersect feature to approximate the number of years it will take before the population of the habitat reaches half its carrying capacity.
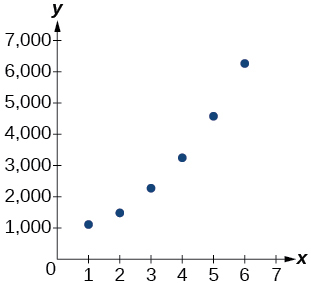
For the following exercises, refer to [link] .
| x | f(x) |
| 1 | 1125 |
| 2 | 1495 |
| 3 | 2310 |
| 4 | 3294 |
| 5 | 4650 |
| 6 | 6361 |
Use a graphing calculator to create a scatter diagram of the data.
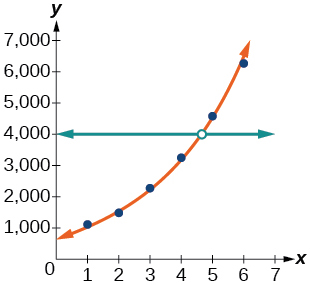
Use the regression feature to find an exponential function that best fits the data in the table.
Write the exponential function as an exponential equation with base
Graph the exponential equation on the scatter diagram.
Use the intersect feature to find the value of for which
When
For the following exercises, refer to [link] .
| x | f(x) |
| 1 | 555 |
| 2 | 383 |
| 3 | 307 |
| 4 | 210 |
| 5 | 158 |
| 6 | 122 |
Use a graphing calculator to create a scatter diagram of the data.

Notification Switch
Would you like to follow the 'College algebra' conversation and receive update notifications?