| << Chapter < Page | Chapter >> Page > |
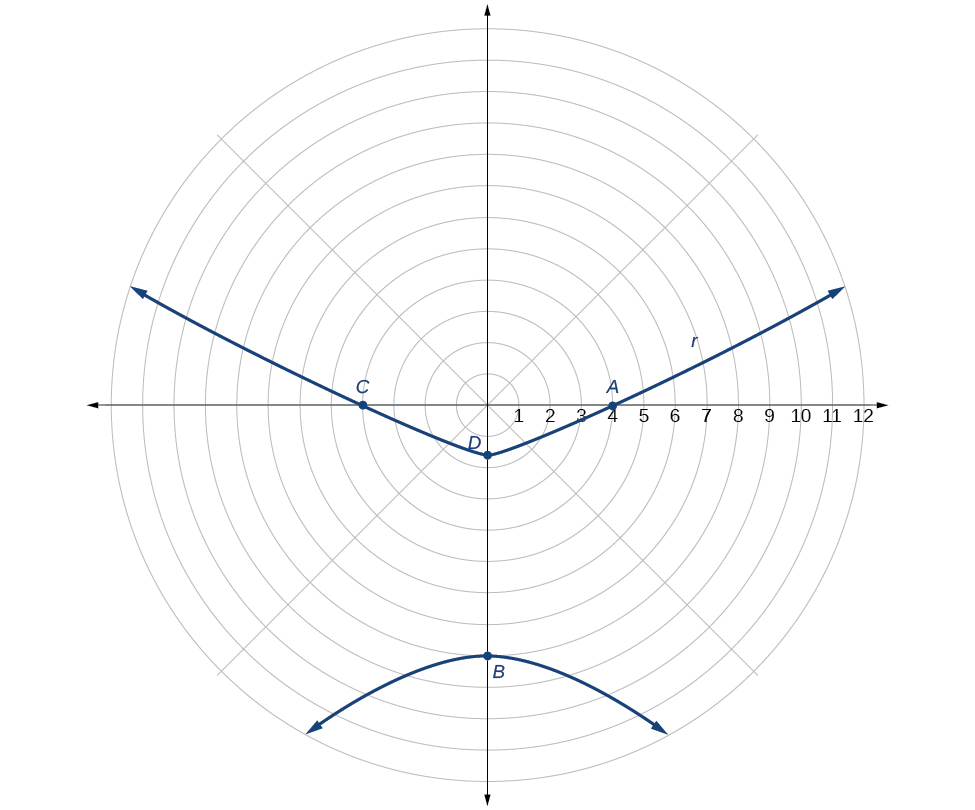
Graph
First, we rewrite the conic in standard form by multiplying the numerator and denominator by the reciprocal of 2, which is
Because so we will graph a hyperbola with a focus at the origin. The function has a term and there is a subtraction sign in the denominator, so the directrix is
The directrix is
Plotting a few key points as in [link] will enable us to see the vertices. See [link] .
| A | B | C | D | |
|---|---|---|---|---|
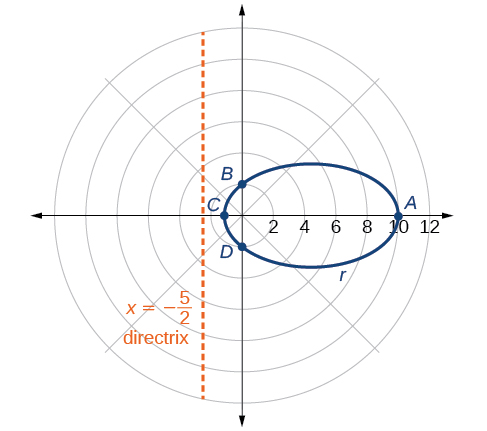
Graph
First, we rewrite the conic in standard form by multiplying the numerator and denominator by the reciprocal of 5, which is
Because so we will graph an ellipse with a focus at the origin. The function has a and there is a subtraction sign in the denominator, so the directrix is
The directrix is
Plotting a few key points as in [link] will enable us to see the vertices. See [link] .
| A | B | C | D | |
|---|---|---|---|---|
So far we have been using polar equations of conics to describe and graph the curve. Now we will work in reverse; we will use information about the origin, eccentricity, and directrix to determine the polar equation.
Given the focus, eccentricity, and directrix of a conic, determine the polar equation.
Find the polar form of the conic given a focus at the origin, and directrix
The directrix is so we know the trigonometric function in the denominator is sine.
Because so we know there is a subtraction sign in the denominator. We use the standard form of
and and
Therefore,
Find the polar form of a conic given a focus at the origin, and directrix
Because the directrix is we know the function in the denominator is cosine. Because so we know there is an addition sign in the denominator. We use the standard form of
and and
Therefore,
Find the polar form of the conic given a focus at the origin, and directrix

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?