| << Chapter < Page | Chapter >> Page > |
Use grouping to factor and solve the quadratic equation:
First, multiply Then list the factors of
The only pair of factors that sums to is Rewrite the equation replacing the b term, with two terms using 3 and 12 as coefficients of x . Factor the first two terms, and then factor the last two terms.
Solve using the zero-product property.
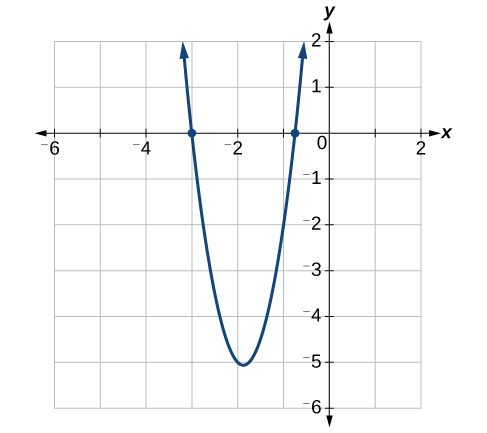
The solutions are See [link] .
Solve the equation by factoring:
This equation does not look like a quadratic, as the highest power is 3, not 2. Recall that the first thing we want to do when solving any equation is to factor out the GCF, if one exists. And it does here. We can factor out from all of the terms and then proceed with grouping.
Use grouping on the expression in parentheses.
Now, we use the zero-product property. Notice that we have three factors.
The solutions are and
When there is no linear term in the equation, another method of solving a quadratic equation is by using the square root property , in which we isolate the term and take the square root of the number on the other side of the equals sign. Keep in mind that sometimes we may have to manipulate the equation to isolate the term so that the square root property can be used.
With the term isolated, the square root property states that:
where k is a nonzero real number.
Given a quadratic equation with an term but no term, use the square root property to solve it.
Solve the quadratic using the square root property:
Take the square root of both sides, and then simplify the radical. Remember to use a sign before the radical symbol.
The solutions are
Solve the quadratic equation:
First, isolate the term. Then take the square root of both sides.
The solutions are
Solve the quadratic equation using the square root property:
Not all quadratic equations can be factored or can be solved in their original form using the square root property. In these cases, we may use a method for solving a quadratic equation known as completing the square . Using this method, we add or subtract terms to both sides of the equation until we have a perfect square trinomial on one side of the equal sign. We then apply the square root property. To complete the square, the leading coefficient, a , must equal 1. If it does not, then divide the entire equation by a . Then, we can use the following procedures to solve a quadratic equation by completing the square.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?