| << Chapter < Page | Chapter >> Page > |
What role does the horizontal asymptote of an exponential function play in telling us about the end behavior of the graph?
An asymptote is a line that the graph of a function approaches, as either increases or decreases without bound. The horizontal asymptote of an exponential function tells us the limit of the function’s values as the independent variable gets either extremely large or extremely small.
What is the advantage of knowing how to recognize transformations of the graph of a parent function algebraically?
The graph of is reflected about the y -axis and stretched vertically by a factor of What is the equation of the new function, State its y -intercept, domain, and range.
y -intercept: Domain: all real numbers; Range: all real numbers greater than
The graph of is reflected about the y -axis and compressed vertically by a factor of What is the equation of the new function, State its y -intercept, domain, and range.
The graph of is reflected about the x -axis and shifted upward units. What is the equation of the new function, State its y -intercept, domain, and range.
y -intercept: Domain: all real numbers; Range: all real numbers less than
The graph of is shifted right units, stretched vertically by a factor of reflected about the x -axis, and then shifted downward units. What is the equation of the new function, State its y -intercept (to the nearest thousandth), domain, and range.
The graph of is shifted left units, stretched vertically by a factor of reflected about the x -axis, and then shifted downward units. What is the equation of the new function, State its y -intercept, domain, and range.
y -intercept: Domain: all real numbers; Range: all real numbers greater than
For the following exercises, graph the function and its reflection about the y -axis on the same axes, and give the y -intercept.
For the following exercises, graph each set of functions on the same axes.
For the following exercises, match each function with one of the graphs in [link] .
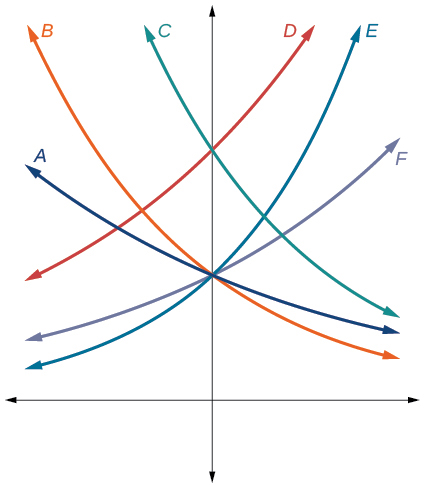
For the following exercises, use the graphs shown in [link] . All have the form
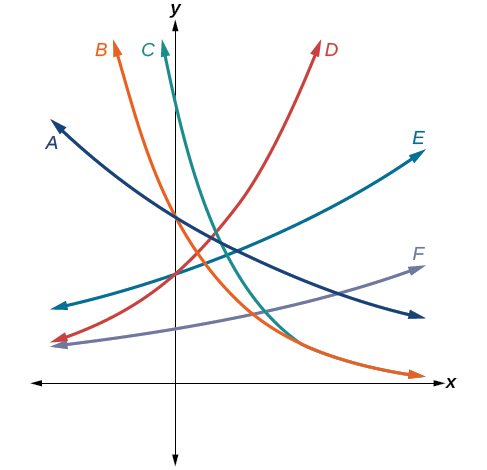
Which graph has the smallest value for
Which graph has the smallest value for
For the following exercises, graph the function and its reflection about the x -axis on the same axes.
For the following exercises, graph the transformation of Give the horizontal asymptote, the domain, and the range.
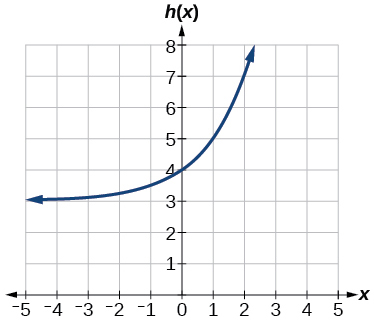
Horizontal asymptote: Domain: all real numbers; Range: all real numbers strictly greater than
For the following exercises, describe the end behavior of the graphs of the functions.
For the following exercises, start with the graph of Then write a function that results from the given transformation.
Shift 4 units upward
Shift 2 units left
Reflect about the x -axis
For the following exercises, each graph is a transformation of Write an equation describing the transformation.
For the following exercises, find an exponential equation for the graph.
For the following exercises, evaluate the exponential functions for the indicated value of
For the following exercises, use a graphing calculator to approximate the solutions of the equation. Round to the nearest thousandth.
Explore and discuss the graphs of and Then make a conjecture about the relationship between the graphs of the functions and for any real number
The graph of is the refelction about the y -axis of the graph of For any real number and function the graph of is the the reflection about the y -axis,
Prove the conjecture made in the previous exercise.
Explore and discuss the graphs of and Then make a conjecture about the relationship between the graphs of the functions and for any real number n and real number
The graphs of and are the same and are a horizontal shift to the right of the graph of For any real number n , real number and function the graph of is the horizontal shift
Prove the conjecture made in the previous exercise.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?