| << Chapter < Page | Chapter >> Page > |
Use synthetic division to divide by
Begin by setting up the synthetic division. Write and the coefficients.

Bring down the lead coefficient. Multiply the lead coefficient by
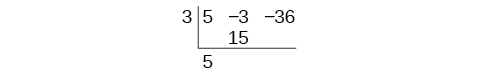
Continue by adding the numbers in the second column. Multiply the resulting number by Write the result in the next column. Then add the numbers in the third column.
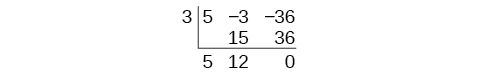
The result is The remainder is 0. So is a factor of the original polynomial.
Use synthetic division to divide by
The binomial divisor is so Add each column, multiply the result by –2, and repeat until the last column is reached.
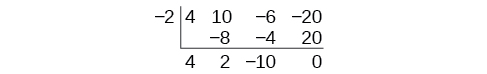
The result is The remainder is 0. Thus, is a factor of
Use synthetic division to divide by
Notice there is no
x -term. We will use a zero as the coefficient for that term.
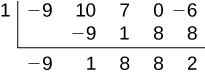
The result is
Polynomial division can be used to solve a variety of application problems involving expressions for area and volume. We looked at an application at the beginning of this section. Now we will solve that problem in the following example.
The volume of a rectangular solid is given by the polynomial The length of the solid is given by and the width is given by Find the height, of the solid.
There are a few ways to approach this problem. We need to divide the expression for the volume of the solid by the expressions for the length and width. Let us create a sketch as in [link] .
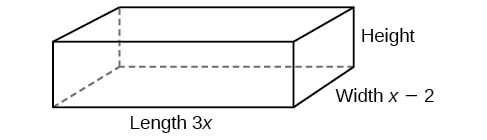
We can now write an equation by substituting the known values into the formula for the volume of a rectangular solid.
To solve for first divide both sides by
Now solve for using synthetic division.

The quotient is and the remainder is 0. The height of the solid is
The area of a rectangle is given by The width of the rectangle is given by Find an expression for the length of the rectangle.
Access these online resources for additional instruction and practice with polynomial division.
| Division Algorithm |

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?