| << Chapter < Page | Chapter >> Page > |
The degree of a polynomial function helps us to determine the number of x -intercepts and the number of turning points. A polynomial function of degree is the product of factors, so it will have at most roots or zeros, or x -intercepts. The graph of the polynomial function of degree must have at most turning points. This means the graph has at most one fewer turning point than the degree of the polynomial or one fewer than the number of factors.
A continuous function has no breaks in its graph: the graph can be drawn without lifting the pen from the paper. A smooth curve is a graph that has no sharp corners. The turning points of a smooth graph must always occur at rounded curves. The graphs of polynomial functions are both continuous and smooth.
A polynomial of degree will have, at most, x -intercepts and turning points.
Without graphing the function, determine the local behavior of the function by finding the maximum number of x -intercepts and turning points for
The polynomial has a degree of so there are at most 10 x -intercepts and at most 9 turning points.
Without graphing the function, determine the maximum number of x -intercepts and turning points for
There are at most 12 intercepts and at most 11 turning points.
What can we conclude about the polynomial represented by the graph shown in [link] based on its intercepts and turning points?

The end behavior of the graph tells us this is the graph of an even-degree polynomial. See [link] .
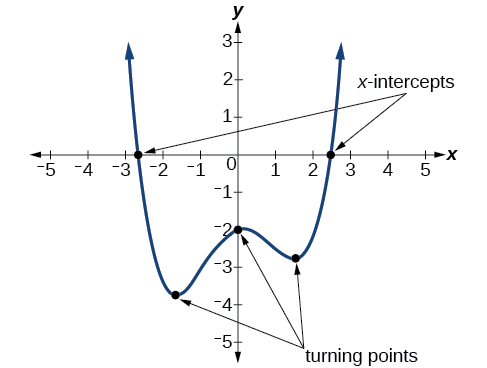
The graph has 2 x -intercepts, suggesting a degree of 2 or greater, and 3 turning points, suggesting a degree of 4 or greater. Based on this, it would be reasonable to conclude that the degree is even and at least 4.
What can we conclude about the polynomial represented by the graph shown in [link] based on its intercepts and turning points?
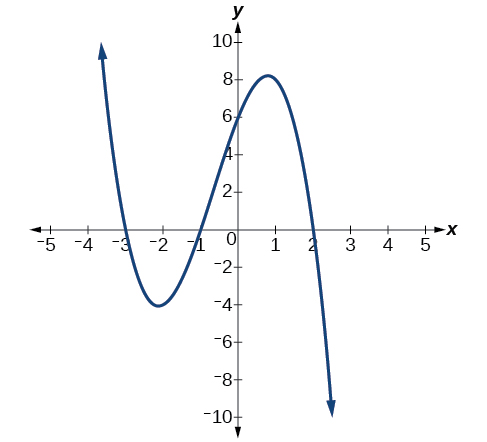
The end behavior indicates an odd-degree polynomial function; there are 3 intercepts and 2 turning points, so the degree is odd and at least 3. Because of the end behavior, we know that the lead coefficient must be negative.
Given the function determine the local behavior.
The y -intercept is found by evaluating
The y -intercept is
The x -intercepts are found by determining the zeros of the function.
The x -intercepts are and
The degree is 3 so the graph has at most 2 turning points.
Given the function determine the local behavior.
The intercepts are and the y- intercept is and the graph has at most 2 turning points.
Access these online resources for additional instruction and practice with power and polinomial functions.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?