| << Chapter < Page | Chapter >> Page > |
Given data of input and corresponding outputs from a linear function, find the best fit line using linear regression.
Find the least squares regression line using the cricket-chirp data in [link] .
| L1 | 44 | 35 | 20.4 | 33 | 31 | 35 | 18.5 | 37 | 26 |
| L2 | 80.5 | 70.5 | 57 | 66 | 68 | 72 | 52 | 73.5 | 53 |
Will there ever be a case where two different lines will serve as the best fit for the data?
No. There is only one best fit line.
As we saw above with the cricket-chirp model, some data exhibit strong linear trends, but other data, like the final exam scores plotted by age, are clearly nonlinear. Most calculators and computer software can also provide us with the correlation coefficient , which is a measure of how closely the line fits the data. Many graphing calculators require the user to turn a ”diagnostic on” selection to find the correlation coefficient, which mathematicians label as The correlation coefficient provides an easy way to get an idea of how close to a line the data falls.
We should compute the correlation coefficient only for data that follows a linear pattern or to determine the degree to which a data set is linear. If the data exhibits a nonlinear pattern, the correlation coefficient for a linear regression is meaningless. To get a sense for the relationship between the value of and the graph of the data, [link] shows some large data sets with their correlation coefficients. Remember, for all plots, the horizontal axis shows the input and the vertical axis shows the output.
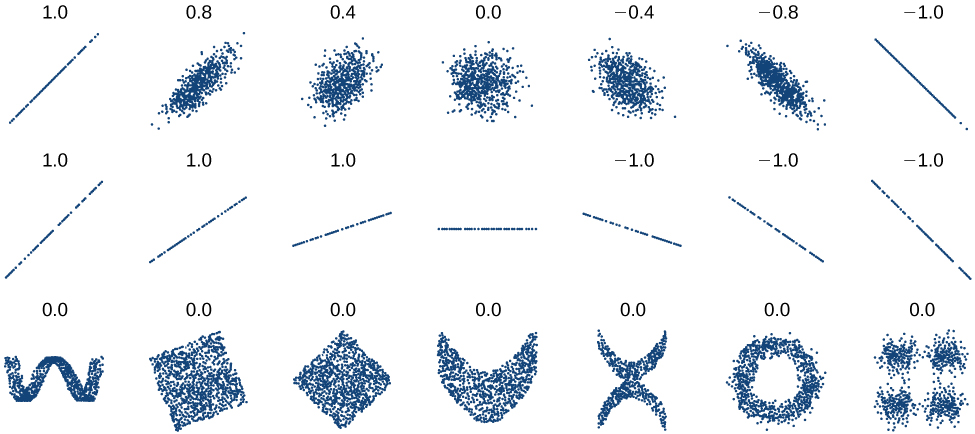
The correlation coefficient is a value, between –1 and 1.
Calculate the correlation coefficient for cricket-chirp data in [link] .
Because the data appear to follow a linear pattern, we can use technology to calculate Enter the inputs and corresponding outputs and select the Linear Regression. The calculator will also provide you with the correlation coefficient, This value is very close to 1, which suggests a strong increasing linear relationship.
Note: For some calculators, the Diagnostics must be turned "on" in order to get the correlation coefficient when linear regression is performed: [2nd]>[0]>[alpha][x–1], then scroll to DIAGNOSTICSON.
Once we determine that a set of data is linear using the correlation coefficient, we can use the regression line to make predictions. As we learned above, a regression line is a line that is closest to the data in the scatter plot, which means that only one such line is a best fit for the data.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?