| << Chapter < Page | Chapter >> Page > |
A man has 72 ft. of fencing to put around a rectangular garden. If the length is 3 times the width, find the dimensions of his garden.
A truck rental is $25 plus $.30/mi. Find out how many miles Ken traveled if his bill was $50.20.
84 mi
For the following exercises, use the quadratic equation to solve.
For the following exercises, name the horizontal component and the vertical component.
For the following exercises, perform the operations indicated.
For the following exercises, solve the quadratic equation by factoring.
For the following exercises, solve the quadratic equation by using the square-root property.
For the following exercises, solve the quadratic equation by completing the square.
For the following exercises, solve the quadratic equation by using the quadratic formula. If the solutions are not real, state No real solution .
For the following exercises, solve the quadratic equation by the method of your choice.
For the following exercises, solve the equations.
For the following exercises, solve the inequality. Write your final answer in interval notation.
For the following exercises, solve the compound inequality. Write your answer in interval notation.
For the following exercises, graph as described.
Graph the absolute value function and graph the constant function. Observe the points of intersection and shade the x -axis representing the solution set to the inequality. Show your graph and write your final answer in interval notation.
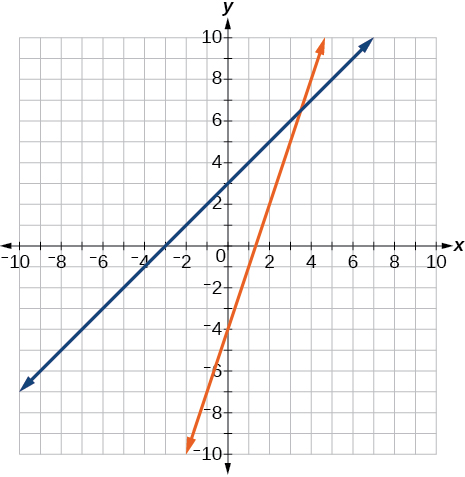
Graph both straight lines (left-hand side being y1 and right-hand side being y2) on the same axes. Find the point of intersection and solve the inequality by observing where it is true comparing the y -values of the lines. See the interval where the inequality is true.
Where the blue is below the orange line; point of intersection is
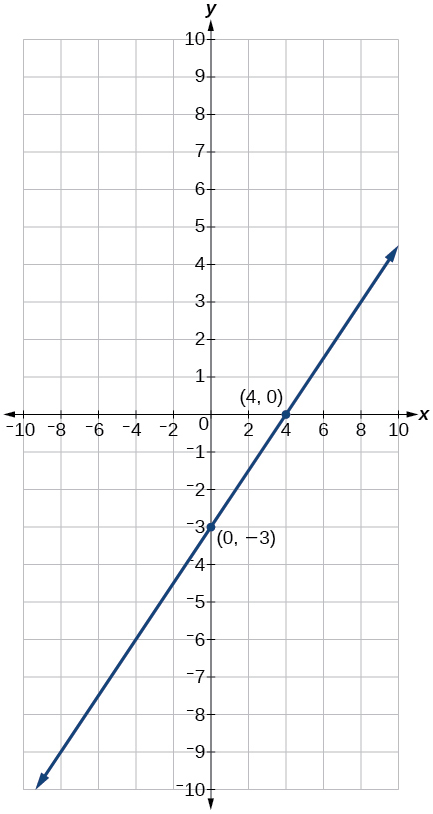
Find the x- and y -intercepts of this equation, and sketch the graph of the line using just the intercepts plotted.
Find the exact distance between and Find the coordinates of the midpoint of the line segment joining the two points.
Write the interval notation for the set of numbers represented by
Solve for x :
Solve for x :
The perimeter of a triangle is 30 in. The longest side is 2 less than 3 times the shortest side and the other side is 2 more than twice the shortest side. Find the length of each side.
For the following exercises, find the equation of the line with the given information.
Has an undefined slope and passes through the point
Add these complex numbers:
Multiply:
Solve this quadratic equation and write the two complex roots in form:
For the following exercises, find the real solutions of each equation by factoring.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?